Amber tutorial - Protein Ligand binding free energies

Small molecule binding to T4-lysozyme L99A

This is the final part of this tutorial, concerned with analysing the MD runs and constructing and interpreting the free energy curves. The first page with background information is available here, the second one with system setup information here

Running and Analyzing the MD simulations

After running all the simulations outlined in the previous page, we obtain a tremendous amount of output data. This section shows how to analyze this so that we finally obtain an estimate of the relative binding free energy of our two ligands. A first step would be to take a look a the amber mdout files, to see if anything went terribly wrong with our physical parameters. The following tables give an overview over the output files from the six different simulations:

Transformation: Remove charges from BNZ H6 - Medium: Water

Lambda	DVDL	rms	ksteps	TEMP	rms	PRESS	rms	Density	rms	Filename
0.100	-5.424	1.193	100	299.55	5.96	2.8	360.7	0.9842	0.0038	bnz_prod_v0_l1.out
0.200	-5.774	1.200	100	299.80	5.94	0.3	361.2	0.9833	0.0033	bnz_prod_v0_l2.out
0.300	-5.968	1.199	100	300.07	6.23	-0.7	358.2	0.9834	0.0042	bnz_prod_v0_l3.out
0.400	-6.205	1.213	100	299.31	5.99	1.4	356.7	0.9839	0.0038	bnz_prod_v0_l4.out
0.500	-6.488	1.250	100	299.50	5.95	1.9	347.2	0.9820	0.0035	bnz_prod_v0_l5.out
0.600	-6.681	1.261	100	299.46	5.90	-0.7	354.5	0.9841	0.0037	bnz_prod_v0_l6.out
0.700	-6.977	1.281	100	299.53	6.23	0.7	357.2	0.9844	0.0032	bnz_prod_v0_l7.out
0.800	-7.279	1.299	100	300.38	6.06	1.0	354.6	0.9818	0.0043	bnz_prod_v0_l8.out
0.900	-7.445	1.308	100	300.14	6.07	4.9	357.4	0.9835	0.0043	bnz_prod_v0_l9.out

Transformation: Transform BNZ into PHN - Medium: Water

Lambda	DVDL	rms	ksteps	TEMP	rms	PRESS	rms	Density	rms	Filename
0.100	5.188	3.076	100	300.01	5.94	0.6	354.1	0.9824	0.0040	bnz_prod_v0_l1.out
0.200	4.404	3.033	100	300.29	5.82	2.3	354.0	0.9832	0.0037	bnz_prod_v0_l2.out
0.300	3.660	3.010	100	299.67	5.97	-0.4	359.0	0.9835	0.0036	bnz_prod_v0_l3.out
0.400	2.523	3.112	100	299.80	6.06	-0.8	357.1	0.9817	0.0045	bnz_prod_v0_l4.out
0.500	1.367	3.188	100	300.24	6.09	-0.1	357.6	0.9830	0.0038	bnz_prod_v0_l5.out
0.600	0.602	3.468	100	299.52	6.04	-1.2	362.6	0.9820	0.0036	bnz_prod_v0_l6.out
0.700	-0.598	3.275	100	299.97	6.13	-0.3	359.5	0.9831	0.0037	bnz_prod_v0_l7.out
0.800	-1.757	3.102	100	300.21	6.15	4.1	368.2	0.9841	0.0041	bnz_prod_v0_l8.out
0.900	-2.695	2.989	100	299.84	6.01	2.7	357.4	0.9817	0.0037	bnz_prod_v0_l9.out

Transformation: Add charges to PHN O1,H6 - Medium: Water

Lambda	DVDL	rms	ksteps	TEMP	rms	PRESS	rms	Density	rms	Filename
0.100	-29.498	2.153	100	299.78	6.07	2.3	356.8	0.9850	0.0032	phn_prod_v0_l1.out
0.200	-30.213	2.233	100	299.92	6.05	0.0	361.6	0.9834	0.0038	phn_prod_v0_l2.out
0.300	-31.081	2.330	100	300.03	6.08	0.9	361.2	0.9835	0.0040	phn_prod_v0_l3.out
0.400	-32.142	2.486	100	300.34	5.95	1.3	350.8	0.9831	0.0033	phn_prod_v0_l4.out
0.500	-32.923	2.598	100	300.49	5.94	0.1	356.1	0.9824	0.0035	phn_prod_v0_l5.out
0.600	-34.052	2.774	100	300.45	6.02	0.8	352.7	0.9833	0.0041	phn_prod_v0_l6.out
0.700	-35.768	3.075	100	300.12	6.17	1.3	357.9	0.9826	0.0042	phn_prod_v0_l7.out
0.800	-37.675	3.415	100	300.21	5.93	-1.1	357.9	0.9826	0.0036	phn_prod_v0_l8.out
0.900	-39.873	3.655	100	300.49	6.06	3.0	364.9	0.9831	0.0041	phn_prod_v0_l9.out

Transformation: Remove charges from BNZ H6 - Medium: Protein

Lambda	DVDL	rms	ksteps	TEMP	rms	PRESS	rms	Density	rms	Filename
0.100	-5.380	0.697	100	299.99	1.67	0.2	135.8	1.0126	0.0011	t4_bnz_prod_v0_l1.out
0.200	-6.381	0.726	100	300.04	1.70	2.1	134.0	1.0125	0.0012	t4_bnz_prod_v0_l2.out
0.300	-5.967	0.823	100	299.87	1.70	0.9	136.0	1.0130	0.0012	t4_bnz_prod_v0_l3.out
0.400	-6.368	0.831	100	299.90	1.67	0.6	136.8	1.0127	0.0011	t4_bnz_prod_v0_l4.out
0.500	-6.502	0.733	100	300.02	1.68	1.6	133.1	1.0131	0.0010	t4_bnz_prod_v0_l5.out
0.600	-6.887	0.712	100	300.19	1.63	0.1	137.5	1.0127	0.0013	t4_bnz_prod_v0_l6.out
0.700	-6.747	0.764	100	300.09	1.71	1.1	135.7	1.0130	0.0011	t4_bnz_prod_v0_l7.out
0.800	-6.885	0.803	100	300.02	1.67	0.8	136.0	1.0128	0.0011	t4_bnz_prod_v0_l8.out
0.900	-7.104	0.766	100	300.15	1.68	1.5	137.6	1.0131	0.0013	t4_bnz_prod_v0_l9.out

Transformation: Transform BNZ into PHN - Medium: Protein

Lambda	DVDL	rms	ksteps	TEMP	rms	PRESS	rms	Density	rms	Filename
0.100	2.213	2.198	100	299.99	1.67	1.9	135.1	1.0129	0.0012	t4_bnz_prod_v0_l1.out
0.200	2.511	2.078	100	299.97	1.66	1.1	134.5	1.0128	0.0012	t4_bnz_prod_v0_l2.out
0.300	3.504	2.000	100	299.87	1.70	0.8	134.6	1.0130	0.0011	t4_bnz_prod_v0_l3.out
0.400	3.975	2.314	100	300.05	1.68	1.3	134.7	1.0130	0.0011	t4_bnz_prod_v0_l4.out
0.500	4.160	2.997	100	300.16	1.71	1.5	137.4	1.0126	0.0014	t4_bnz_prod_v0_l5.out
0.600	3.330	3.413	100	300.29	1.72	2.0	133.4	1.0126	0.0011	t4_bnz_prod_v0_l6.out
0.700	2.957	3.247	100	300.14	1.72	1.1	135.5	1.0128	0.0013	t4_bnz_prod_v0_l7.out
0.800	0.988	2.943	100	300.16	1.69	1.8	133.3	1.0128	0.0013	t4_bnz_prod_v0_l8.out
0.900	3.490	3.524	100	300.03	1.67	1.2	135.8	1.0124	0.0011	t4_bnz_prod_v0_l9.out

Transformation: Add charges to PHN O1,H6 - Medium: Protein

Lambda	DVDL	rms	ksteps	TEMP	rms	PRESS	rms	Density	rms	Filename
0.100	-32.831	1.170	100	300.00	1.69	1.9	132.4	1.0129	0.0011	t4_phn_prod_v0_l1.out
0.200	-33.164	1.169	100	300.09	1.66	0.4	134.2	1.0126	0.0013	t4_phn_prod_v0_l2.out
0.300	-33.385	1.322	100	300.00	1.72	0.7	133.9	1.0126	0.0012	t4_phn_prod_v0_l3.out
0.400	-33.828	1.271	100	299.98	1.74	1.1	135.0	1.0127	0.0012	t4_phn_prod_v0_l4.out
0.500	-33.840	1.247	100	300.06	1.69	0.6	136.6	1.0128	0.0012	t4_phn_prod_v0_l5.out
0.600	-34.164	1.189	100	300.00	1.68	1.3	134.9	1.0133	0.0011	t4_phn_prod_v0_l6.out
0.700	-34.454	1.293	100	299.98	1.69	1.9	137.1	1.0130	0.0013	t4_phn_prod_v0_l7.out
0.800	-34.659	1.341	100	300.01	1.70	1.1	137.7	1.0127	0.0015	t4_phn_prod_v0_l8.out
0.900	-34.388	1.318	100	299.93	1.67	1.1	133.9	1.0131	0.0011	t4_phn_prod_v0_l9.out

We see temperature fluctuation in the range of 5K for the ligands in water and 2K for the complexes, about what one would expect. The pressures fluctuate wildly as always when ntp=2 is used, but densities stay relatively constant. dV/dλ rms values are in the range of several kcal/mol. In an actual study, this quick glance over the results would need to be replaced with a careful analysis of all the trajectories to see if interesting conformational changes or ligand movements happen, but it shall suffice for the purpose of this tutorial. Therefore we can proceed to analysing the resulting dV/dλ vs. λ curves.

Results

The plot below shows the dV/dλ curves assembled from 9 λ points each. We can see that the curves for transformations in water are smoother than those for the ligand change in the protein, as would be expected due to the more complex conformational landscape of a protein-ligand complex as compared to an isotropic solution. The vdW-transformation in the complex shows the biggest fluctuations of dV/dλ and the free energy curve for Step 2 in the complex is the one that looks the most 'bumpy'. Since TI-free energy curves are almost always smooth curves, this can probably be attributed to insufficient sampling and running longer simulations for the transformations in complex would most likely smooth out the free energy curves considerably.

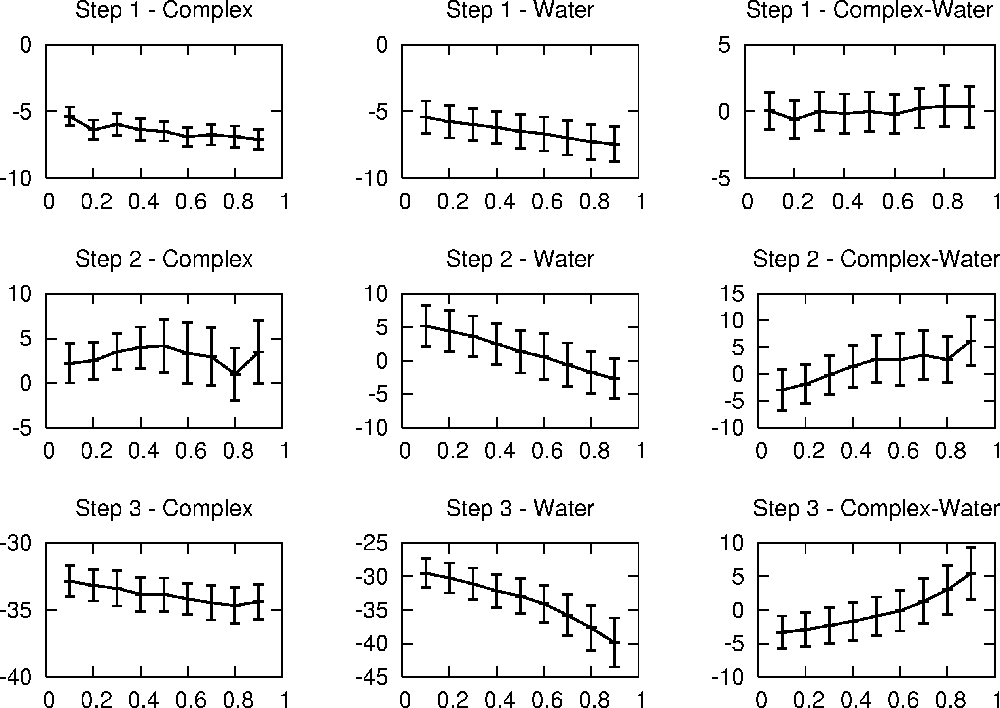
The thermodynamic effect of removing the charge on the hydrogen atom is small and very similar when done in complex or solution. Adding the charges to the phenyl group (step 3) gives much bigger changes in energy than the other two steps, but bear in mind that the result of a single transformation is not a physically significant number, only differences between the results of two transformations are. The free energy change associated with each of the steps can be calculated by numerically integrating over the ΔG(Complex-Water) curves on the right from λ=0-1. The integration can e.g. be done using this script on a list with λ, dV/dλ and rms(dV/dλ) values like that one). The trapezoid rule (values for λ=0 and 1 were linearly extrapolated from the closest two values) gives:

Step	Free Energy change	rms

ΔG (Step 1)	0.05	1.46
ΔG (Step 2)	1.72	4.19
ΔG (Step 3)	0.06	3.04

ΔG (Total)	1.83	5.34

Interestingly, the main contribution to the binding free energy difference stems from vdW interactions and not from electrostatics. One would have expected that the loss of solvation on the polar hydroxyl group might strongly influence the relative binding free energies, but from this calculations, the main difference seems to be the sterical effect of accomodating the bulkier hydroxyl group in the binding site, with electrostatics playing a minor role. This result might however change if the calculation would be refined further.
Our prediction is that phenol binds 1.8 kcal/mol weaker to T4-lysozyme than benzene. While this is not in perfect agreement with experimental data, it captures the trend of benzene being the stronger binder. To improve the result, more simulations could be added at different λ points (this is indeed one of the strong points of TI, you can add as many additional data points as you want to refine your result without having to redo the initial calculations) or more sophisticated numerical integration schemes could be used. The rms value of the final result should not be mistaken for the statistical uncertainty of the result. To get a good error estimation, some additional analysis is required (see e.g. Steinbrecher T. et al., J Chem. Phys. 127, 214108, 2008).

This tutorial was written by Thomas Steinbrecher, TSRI 2007