Small molecule binding to T4-lysozyme L99A

Setting up the System

The two ligands were sketched and parametrized with gaff atom types and resp charges were generated using antechamber on gaussian03 output files. (Please refer to tutorial 4 on how to use the antechamber tools to parametrize a ligand. The benzene and phenol molecules were saved in two OFF-libraries (benz.lib and phen.lib) for further use. The screenshot shows that C6 was selected as the position bearing the hydroxyl group in phenol.

We will use the X-ray structure of T4-L99A from the pdb (after stripping water molecules and unneeded heteroatoms from it: pdb file) as basis to set up our simulation files. We will use two runs of leap to produce four set of parameter and restart files, containing both ligands in the protein bound and solvated states. The first leap run (input file) will produce pdb files of the solvated und neutralized benzene complex and of the benzene ligand in water (complex.pdb and ligand.pdb). From these two additional pdb files are made by renaming the BNZ molecule to PHN and deleting H6 (t4_phn.pdb and phn.pdb). These four pdb files are then used in a second leap run (input file) to generate the *.prm and *.rst files. This yields 4 parameter and 4 rst files

	benzene	phenol
complex	prm/rst	prm/rst
solvated ligand	prm/rst	prm/rst

There is a reason why we use this confusing two step process to build the parameter files. In out later TI runs, the two parameter files for the different ligands will be coupled and propagated according to the combined potential V(λ). Both processes will have a set of atoms that are unique to them (which are H6 in the benzene and O1 and H6 in the phenol case) as well as a set of common atoms (water, the rest of the aromatic ring and the protein in the bound systems). It is required that all common atoms in both input files have identical starting coordinates and appear in the same order and if we just used solvatebox on two different ligands (even if they differ only by a few atoms) water molecules would be added in quite different positions.
Alternatively, one could build one of the systems in leap and then modify it into the other by adding/deleting atoms and bonds. The only important thing is that in the final input files, all coordinates for atoms common to both processes (as well as the box sizes) are identical (or close to identical, you can get away with small coordinate deviations due to e.g. rounding errors which will be corrected during sander startup with a warning message). Please note that no special type of prmtop files (as in Amber7) or balancing of atom numbers with dummy atoms (as in Amber9) is necessary for setup.

Input file preparation

Two different ligand transformations need to be simulated, benzene to phenol in water and bound to lysozyme (Simulating a 'back' transformation phenol to benzene is not necessary, TI calculations do not have a direction, rather every λ point represents a static intermediate of the transformation). For reasons of simulation consistency, the two transformations are further broken up into three substeps each: First, the atomic partial charge on the hydrogen atom to disappear from benzene are removed, second the ligand vdW-transformation is performed (disappearing or decoupling the benzene hydrogen from its surroundings while simultaneously appearing the phenol hydroxyl group) and finally the phenol hydrogen group gets its atomic partial charges switched on. This is done because having a nonzero charge on an atom while the vdW interactions with its surroundings are getting weakers can lead to simulation instabilities. Also for reasons of simulation consistency, in the van-der-Waals transformation, we will use softcore potentials, a modified LJ-equation that prevents the origin singularity type of free energy divergence from happening (see Simonson T, Mol. Phys 1993: 80:441pp for more information).

The mdin files used for these transformations contain the normal Amber parameters for performing Minimizations/MD simulations that I will not discuss further and in addition to that some unique parameters to perform the TI calculations. The non-TI parts of the input files will perform the following steps:

1. 500 steps of steepest descent minimization (the only kind working with TI)
2. 50 ps of density equilibration (equilibrating T and &delta at the same time is not very good form, but we'll get away with it here
3. 200 ps of NPT production MD to collect dV/dλ data

• icfe=1 to tell sander that this will be a TI run
• clambda=XXX set to the actual value of λ to be used in this run
• ifsc=[0|1] to decide if softcore potentials will be used, indicating appearing and disappearing atoms in the input files
• scmask=='XXX' a mask string set to the atoms that are unique to this process (i.e. disappearing from V0 or appearing in V1, see also the table below)
• crgmask='XXX' a mask string to indicate that some atoms should have their atomic partial charges removed before the simulation starts (This is just for convenience, one could build separate input files in which charges are actually set to zero, which would accomplish the same thing as crgmask)

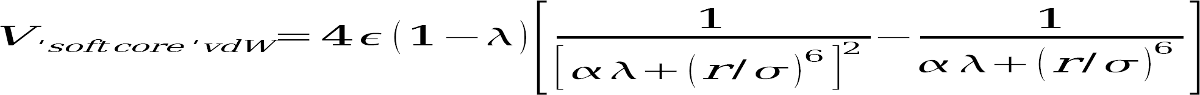
Setting ifsc=1 also informs sander that a number of atoms in each prmtop file (those specified by scmask) shall be considered unique to this potential function. In the step 1 and 3 transformations, we do not need to use softcore potentials, as the only difference between V0 and V1 is the presence or absence of some partial charges, while both start- and endstate have the same number of atoms.
Actually running the simulations will use the multisander functionality of sander.MPI, using e.g.: 'mpirun -np 2 sander.MPI -ng 2 -groupfile group'. Due to the multitude of different input files, it is very advisable to use some sort of script to automate their generation. For example, a simple shell script like this, which sets up the charge removal TI run for benzene in the complex, could serve as a starting point. The script generates a pbs input file that you can adjust for your own brand of supercomputer queueing system. So in the end, a total of two transformations, with three substeps each, with nine λ windows each with three simulations each will be performed, for a total of 162 invocations of the sander module (each using at least two CPUs). A real TI study might involve many more λ windows and significantly longer simulation times, making this a very computationally intensive technique.

This tutorial will continue with a description of running the simulations and analyzing the results here