Free Energy Estimation for Conformers of Dialanine using EMIL

1 Preparing the environment

To test that AMBER is installed type:

in a terminal window. This should return the path to sander, a component of AMBER used for MD simulation. This tutorial requires AMBER 14 or newer.

To test that VMD is installed, type:

or just open the GUI of the program by typing its name.

3 Part I: Simulation using AMBER

3.1 The Conformers of Dialanine

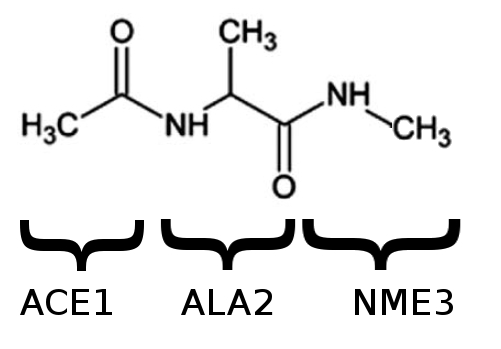
Dialanine is a very small and mostly rigid biological molecule with only two real angular degrees of freedom (fig. 1, 2). It has been intensively studied using many computational and experimental techniques, as a model system to investigate the backbone degrees of freedom which are available to longer protein chains.

Figure 1: The structural formula of our dialanine molecule, showing the residue names assigned by Xleap.

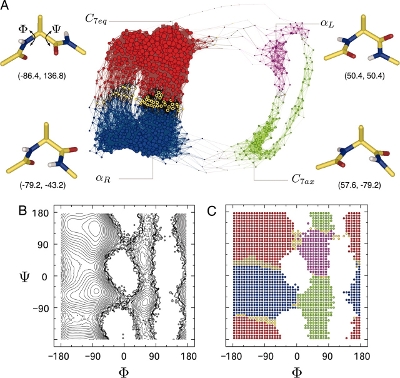
An estimate of the free energy landscape with respect to the two most important degrees of freedom is shown in figure 2. The purpose of this exercise is to test the older calculation using a more detailed and more recent model of the molecule and a different (arguably simpler) method to evaluate the free energy associated with each basin of the free energy landscape.

Figure 2: Dialanine has two dominant degrees of freedom (the dihedral angles labelled Φ and Ψ) yielding four metastable conformations. pic: Gfeller et  al. PNAS 2007. [4]

3.2 Setting up the Dialanine Molecule

Launch AMBER's molecule building tool:

This should open the xleap command window. Xleap goes wrong if NUM-LOCK is active.

In the xleap command window, you can load a set of atom interaction parameters, for instance the 14SB forcefield:

Next, specify the sequence of your molecule:

The ‘capping’ groups ACE and NME are often added at the N terminus (start) and C terminus (end) of a peptide chain, both in experiment and in simulation. Even though there is only one alanine sidechain, we will call the molecule that we have ‘dialanine’, or the ‘alanine dipeptide’, because it has two peptide bonds.

Next, have a look at your molecule:

Nothing to see here, except to make sure that it is the same molecule as the dialanine shown in figure 1. Note that it isn’t exactly the same as the dialanine in fig. 2: the paper which fig. 2 was taken from used a ‘united atom’ representation which treats quasi-rigid groups of atoms as a single spherical atom with increased radius. AMBER ff14SB (like most AMBER forcefields) provides a ‘full atomistic’ representation, where even hydrogen atoms are treated explicitly.

Next, save your molecule m as a pdb file:

Next, save your molecule as AMBER topology and restart files:

Close xleap.

3.3 Running a Simulation In a Dielectric Continuum

Dialanine is a tiny molecule, so we can run a decent molecular dynamics simulation on a normal computer in a matter of minutes. For a more complex system we would first run an energy minimisation, to get rid of any overlaps between atoms, and then slowly thermalise the system in order to allow it to relax into its equilibrium conformation without too much energy being injected at once. For dialanine this isn’t needed.

Save this AMBER input file as "md1ns.in":

You should be able to run sander (or pmemd) straight from the command line:

The arguments above signify: a flag to overwrite previous output, the name of the input file, the top file, the start coordinates, some text-format logging, the trajectory, and the restart file.

You can have a look at the output file while the code is still running (use tail -f diala_md1.out), it gives basic information such as the different terms of the Hamiltonian and the time elapsed. It also gives the instantaneous kinetic temperature: this is not the same as the bath temperature. The bath temperature is fixed, but the kinetic temperature for such a small system will fluctuate a lot.

4 Visualisation using VMD

VMD (Visual Molecular Dynamics) is perhaps the tool most widely used to take a first look at the results of a simulation. It is freely available from Klaus Schulten’s research group in Illinois, but they do ask for a registration. It should already be installed on your computer.

To open your molecule, you can pass VMD the name of the .top file:

You then have to go through some menus to load the trajectory data:

The trajectory file is ‘diala_md1.x’. VMD cannot guess the format, you have to specify that it is “AMBER coordinates”.

The movie that VMD shows is not particularly interesting, the molecule is tumbling around very fast and changing shape seemingly at random. To get some sense, wait until the whole trajectory is loaded and then have a look at the Φ and Ψ angles. Figure 3 shows the definition of the these two angles, each one is specified by an (ordered!) sequence of four backbone atoms. There is only one of each dihedral in our molecule if we ignore atoms from the capping groups.

Figure 3: Peptide dihedral angles. For alanine, the ‘R’ group is just a CH₃. Φ is defined by the sequence C-N-C_α-C, and Ψ is defined by N-C_α-C-N. (Pic from J. Wampler, U. Georgia)

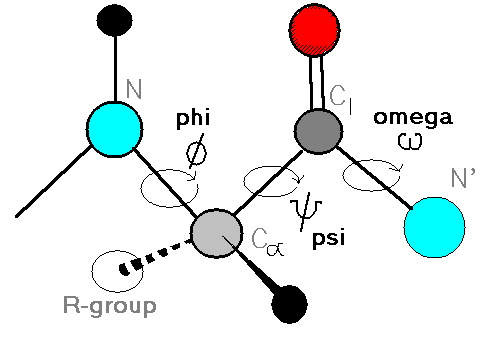
If you press “1”, the vmd cursor will change, and you can use it to bring up atom labels. If you label the six backbone atoms which specify the Φ-Ψ angle pair, then you should be able to use vmd’s dihedral-labelling cursor (“4”), to show the values of the two dihedrals for a given snapshot.

5 Checkpoint for Part 1

Your task for the first half of this lab is to use vmd to make plots of the two dihedral angles and see if you can make sense of these in terms of the plots in figure 2.

You can find a graph-plotting tool in:

As well as having a look at the plots in VMD, you should export the dihedral angle data to two text files so that you can analyse it.

You should try to estimate the free energies of the different wells by brute force, so that you can sanity-check your results from the EMIL calculation later. The free energy of conformational well X is just -kT ln(p(X)).

Use your favourite plotting tool to make histograms of the Φ and Ψ angles to estimate where you should draw the lines between the basins, and then find the probability for the system to be in each well. If the system doesn't visit each well multiple times, then run it for longer. For this rough estimate, you can save a little effort by assuming that the Φ and Ψ distributions are not correlated.

kT at 300 Kelvin is about 0.596 kcal/mol.

6 Part II: Free Energy Estimation Using EMIL

6.1 Introduction and background

The Helmholtz free energy A = U - TS of a system is given by a simple formula:

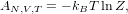
If we write the instantaneous energy of a microstate as the Hamiltonia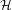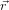n (^N,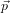 ^N) and set β = 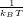then we can write the partition function, Z:

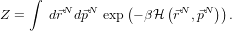
Looking at the partition function, we can make some progress straight away by factorising the integral into terms in the kinetic energy ∑ _i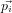²∕m_i and potential energy V :

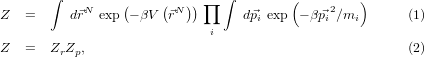
and equipartition gives us Z_p, and thus the free energy component due to thermal motion, straight away.

6.2 Integration Strategy: Make Sure You Understand This Bit

• Consider a system exerting some force, like a gas pushing on a piston of length L, then the time-average force it exerts is:

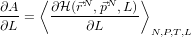
• Now, for dialanine, define a joint Hamiltonian between the ‘real’ system and a reference system for which the free energy is known:

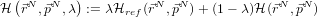
• And use the relation:

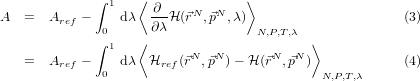
So, after all this, if we can solve (using calculus) the free energy for the reference system 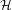_ref, and collect (numerically) some stable time-average values for 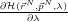over a decent number of points on the interval 0 ≤ λ ≤ 1 , then we can integrate over λ and have the work done to transmute our system into the reference system.

If the reference system and the real system are somewhat like each other, then this integral should be easy to do, and we can estimate the free energy of the real system by this indirect route.

6.3 Setup of System in Each Well

We expect from fig. 2 that there are four metastable conformations for dialanine. To be able to study each one independently, we need to artificially confine a simulation to each of the four basins. To confine a simulation to a given basin, we need to specify a set of restraints and link to them from the main input file.

Create a file md1ns_rest.template.in:

The new information is a pointer to another file to contain restraint specifications, the characters ‘_RESTRAINTS_FILE_’ are just a placeholder. You should also make the following four restraint files:

C7eq.restraints:

alphaL.restraints:

C7ax.restraints:

alphaR.restraints:

6.4 Running Multiple Simulations

To run multiple simulations at the same time, we will use small piece of bash shell scripting:

run_simple.bash:

This should loop over four different systems and start an instance of sander for each. The availablity of this kind of ‘embarrassing parallelism’ is a benefit of EMIL calculations. Type top (q to quit from top) and you should see that four sander processes are running. The term ‘nice’ at the start of the command line sets the priority relatively low, so that the interface of the computer is not frozen by all the calculations it is doing.

Have a look at your output files just to check that the restraints are being activated, e.g.:

If the values are mostly zero, then the system is staying in its metastable basin. It is still good to have a few non-zero values, just to show that the restraints are doing something.

6.5 Definition of Reference System

If the positional part of the system Hamiltonian can be expressed as a sum of non-interacting particles, like this:

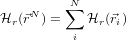
then the free energy A is similarly the sum of one-particle free energies. The Einstein Molecule (EM) is a simple model of a molecular system whereby each atom interacts only with a radial harmonic potential which holds it in place. In this way, the average structure can be the same as that given by a more realistic model but the free energy can be found for each atom as a simple integral.

The value of the reference free energy doesn’t matter for the purpose of this tutorial, as we will be integrating each of our conformations of dialanine to reference states defined in the same way, thus finding the ΔA values between them instead of their absolute free energies.

6.6 Running the calculation

To collect the values of 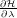we need to run multiple independent simulations at different values of λ, using the EMIL library of AMBER [2]. To do this, we need to make another input file with some extra information:

md_rest_emil.in:

The extra information in this file is just pointers to more EMIL-specific filenames. Because these filenames are going to change, we just put placeholders _LIKE_THIS_ into the file instead of the final values.

Lets have a look at the emil control file, “emilParameters.in”:

emilParameters.in:

Again, this file has some placeholders in it. If you cut and paste this into a text editor and save it, you should be ready to go. Because we are doing multiple runs of EMIL at different values of λ, we will have to use a bit of command-line scripting to launch the jobs:

runEmil.bash:

6.7 Getting the Free Energy

For an expensive calculation, it would be worth making a sophisticated analysis of convergence properties, correlation times etc. in order to get correct errorbars for the estimated energies. See refs  [2] and [3] for some hints on this.

First, plot the time series of generalised forces (the gradients 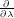) for the separate terms of the Hamiltonian, doing something like this to collect and process the data:

correlatedIntegration.bash:

Run the above script, which should give you a first idea if the calculation has worked or not.

Write your own scripts to make plots of the three terms of the generalised forces and decide if each one has converged to a well-defined average, for each system and each value of lambda.

Do something to find the averages (throwing away data from before convergence) and save your averages to a simple file with λ in column 1 and the total generalised force in column 2 (separately for each system of course).

As you have only a few data points for your integration, it is important to try and make efficient use of them. Ideally something second or third order would be appropriate. Here is a python script to integrate the forces by fitting a spline, rather than the simple Euler method of the previous example:

splineInt.py:

When you have a ΔA for each system, add an offset such that C7_eq is zero and compare the ΔΔA values with the values from Gfeller et. al.[4]. (These values are: α_R = 1.5, C7_ax = 4.1 and α_L = 5.0. They state that their units are kcal/mol.)

7 Next Steps

EMIL was designed and first used for comparing the free energies of systems with substantial conformational differences between them: when there is no easy path of integration from one to the other then an absolute free energy method is the only choice. In such cases there should be no need (or less need) for restraints to define the different free energy basins, such as were used in this tutorial.

The calculation in this tutorial is pretty cheap and fast. To make an explicit-solvent calculation is considerably more expensive: you should use pmemd rather than sander for this. An example of a larger calculation is provided in ref [2], and some more discussion of EMIL with explicit solvent is in [3].

8 FAQ and troubleshooting

• ‘I closed the molecule window and Xleap shut down entirely’: yes, it does that. You have to start again.
• ‘Xleap is acting strangely’: Make sure NUM-lock is off.
• ‘I can’t close VMD’: type quit in the terminal window you launched it from, or close the ‘main’ window by hand.
• ‘How do I kill xxxx job?’. Type ‘top’ to see running jobs and their pids, then ‘kill pid’ to kill the job. Typing ‘killall sander’ should also work.

References