The Nonequilibrium Free Energy (NFE) Toolkit for PMEMD AMBER: Capabilities, Examples, and Collective Variables

By Feng Pan¹, Mahmoud Moradi², Christopher Roland¹ and Celeste Sagui¹

1. Department of Physics, North Carolina State University, Raleigh, NC

2. Department of Chemistry and Biochemistry, University of Arkansas, Fayetteville AR

Abstract

The Nonequilibrium Free Energy (NFE) toolkit, which is fully functional in SANDER, has been partially ported to PMEMD AMBER. The purpose of this tutorial is multifold. We review the current status of the porting of software to PMEMD AMBER v.16, and provide suitable patches for upgrading the toolkit to older versions of AMBER (v.14). Additionally, patches are provided for upgrading modules not released to PMEMD AMBER v.16, and we provide a step-by-step tutorial on how to write new collective variables for free energy calculations. Software templates for new collective variables are also given. Finally, a few examples of using the new PMEMD versions of the code is provided.

Introduction

The NFE toolkit for AMBER grew out of our efforts to speed-up and streamline metadynamics [1,2] for free energy calculations within the context of classical molecular dynamics. The resulting Adaptively Biased Molecular Dynamics (ABMD) method [3,4,5] is characterized by a favorable scaling and time and only a minimal number of control parameters. ABMD calculates free energy landscapes (or more correctly the potential of mean force) as a function of a set of Collective Variables (CVs or colvars) or reaction coordinates that need to be specified. Subsequently, the functionality of NFE suite was enlarged to include multiple walker based simulations, Steered Molecular Dynamics (SMD) [6], Hamiltonian- and Temperature-Replica Exchange Molecular Dynamics (H-REMD, T-REMD) [7], Umbrella Sampling with pre-defined colvars, and most recently the Swarms-of-Trajectories String Method (STSM) [8]. The theory and utility of these algorithms will not be reviewed here (please see the updates to AMBER16 manual - nfe.pdf - or the AMBER17 manual for this). The NFE-based algorithms discussed here were developed by the group of Profs. Celeste Sagui (sagui@ncsu.edu) and Christopher Roland (cmroland@ncsu.edu) with implementation by Dr. Volodymyr Babin. Recent algorithms added to the suite (the selection algorithm based on interacting multiple walkers [9], the well-tempered ABMD (WT-ABMD) [10], driven ABMD (D-ABMD) [11] and STSM [12]) were developed by Prof. Mahmoud Moradi (mmoradi@uark.edu). Testing and porting of the NFE software to PMEMD was by Feng Pan (fpan3@ncsu.edu).

Our current and past papers associated with the NFE-software are:

(i) V. Babin, C. Roland, T.A. Darden and C. Sagui, "The free energy landscape of small peptides as obtained from metadynamics with umbrella sampling corrections", J. Chem. Phys. 125, 204904 (2006);

(ii) V. Babin, C. Roland, and C. Sagui, "Adaptively biased molecular dynamics for free energy calculations", J. Chem. Phys. 128, 134101 (2008);

(iii) V. Babin, V. Karpusenka, M. Moradi, C. Roland, and C. Sagui, "Adaptively biased molecular dynamics: an umbrella sampling method with a time-dependent potential", Int. J. Quant. Chem. 109, 3666 (2009);

(iv) M. Moradi, V. Babin, C. Roland, and C. Sagui, "The adaptively biased molecular dynamics method revisited: new capabilities and an application", J. Phys. Conf. Ser. 640, 012020 (2015).

Current NFE-Modules and their status

The NFE software is currently grouped into 5 modules.

(i) ABMD: which computes free energy maps as a function of 1, 2 (all the way to 5) independent colvars by means of the multiple-walker method (both independent and a new selection algorithm for interacting walkers), and the WT-ABMD.

(ii) BBMD: which has the same functionality as ABMD, but can also carry out H- and T-REMD.

(iii) SMD: can carry out SMD with a self-defined path and variable harmonic constants for a large range of colvars.

(iv) PMD: can carry out Umbrella sampling for the defined colvars, and recently modified enabling using to define the umbrella sampling range.

(v) STSM: carry out the STSM algorithms to calculate the minimum free energy path as a function of several colvars.

Currently, all of these modules have been implemented for SANDER in AMBER. In AMBER v.16, the ABMD and SMD modules have been ported to PMEMD. In the future, we expect to make the newly modified PMD and STSM modules available for PMEMD.

For backwards compatability, patches for these five modules for PMEMD AMBER v.14 are found under this link:

Click here to download the patch for Amber v.14 (Please note that this patch still uses the old format with "ncsu" instead of "nfe", check Amber14 manual for details)

For AMBER v.16 and higher, patches for BBMD, a modified PMD and STSM for PMEMD can be found under this link:

Click here to download the advanced patch for Amber v.16

We note these patches are released `as is'. Note that we do not discuss the STSM module in this tutorial -- this will be the subject of a separate tutorial to be released in the future.

NFE and Collective Variables

The NFE software calculates free energies as a function of a set of pre-defined collective variables or reaction coordinates, which for AMBER are defined in the colvar namelist in a separate file. This tutorial describes how to build such colvars so that they can be used with the different NFE modules. A list of the currently implemented colvars is given collective variable list, with further details on their use given in the AMBER manual. Since we are continuously adding new colvars, we expect to update this list periodically. Specifically, in the coming year we aim to release a set of quaternion-based colvars for the large-scale motions of large numbers of atoms.

A few examples of how to use colvars for different NFE-based simulations can be found collective variable usage examples.

The ability for users to construct their own colvars is important. A short tutorial with a step-by-step example on how to construct colvars for NFE is given under this link:

How to build a new customized Collective Variable

We are happy to incorporate any newly defined and tested colvars for general public use with the NFE suite. Please send these to either sagui@ncsu.edu and fpan3@ncsu.edu.

Some Instructive Examples

We have applied the NFE methodology to a variety of biomolecular systems including small peptides [3,4], sugar puckering [12], polyproline systems [13,14,15] guest-host systems [16,17], polyglutamine [18], and DNA [19] systems. To help jump start the use of the NFE AMBER software, we provide here several examples of its use:

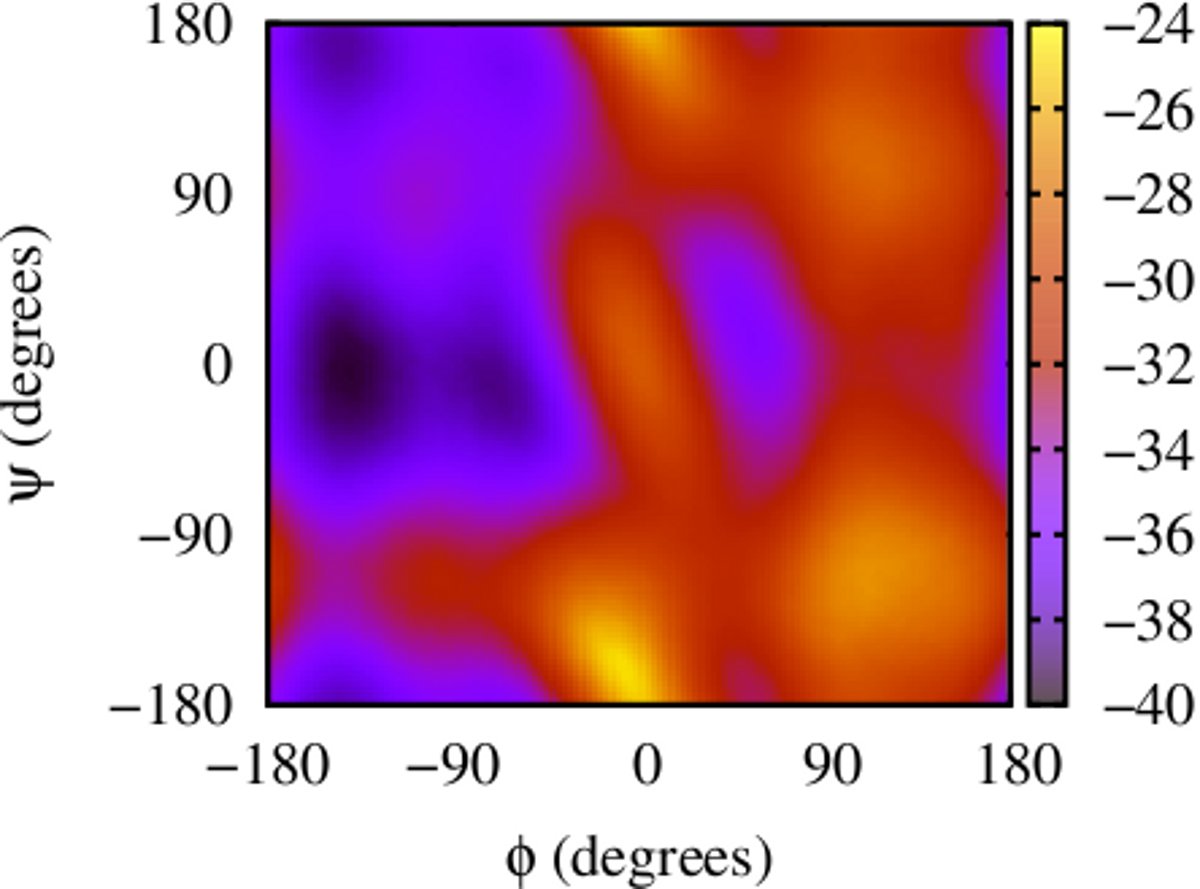
(i) Calculating 2-d free energy landscapes for a di-alanine peptide

Here is an example for running ABMD for a di-alanine peptide in an explicit solvent environment using GPUs with collective variables φ and ψ, to get 2-d free energy landscape. There are two steps to running and the input files and running script can be found here: dialanine-2d-abmd.

Step1: Run a pre-MD simulation of 500ps in the NPT ensemble, obtain 4 trajectories from the last 200ps run as the initial coordinates of the following ABMD

Step2: Run a 50ns ABMD job using multiple-walker method, with selection algorithm and well-tempered algorithm. Here, four replicas are used and run in parallel on four GPUs. The selection constant is set to be 0.00001 and selection frequency is 100ps. The pseudo-temperature is set to be 10000K.

Tips on choosing selection and well-tempered parameters:

There is no standard for choosing the parameters for the selection and well-tempered methods for different systems. Essentially, best parameters need to be chosen based on experience and trial & error. It's probably best to start with a few test runs, and then adjust the parameters till good ones are found.

For the selection algorithm, a larger selection_freq or larger selection_constant will lead to a stronger selection mechanism, which means a more replica duplicating and killing. To reduce the selection mechanism, you need to set a smaller selection_freq or selection_constant, and vice versa. For the well-tempered algorithm, the smaller the wt_temperature(pseudo-temperature) is, the slower and smoother the convergence. To increase the speed of convergence you need to increase wt_temperature; to get a smoother convergence, you need to decrease the wt_temperature.

The result gives the 2-D Free Energy landscape:

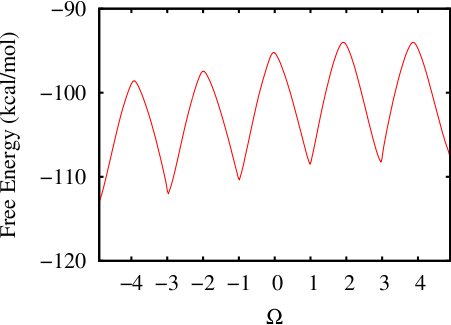
(ii) Calculating 1-d free energy profile of a proline pentapeptide

This example has been shown in details in TUTORIAL A12 using H-REMD ABMD in implicit solvent. Here we provide a rerun of this system using regular multiple-walker ABMD with well-tempered algorithm in an explicit solvent environment. The same colletive variable COS_OF_DIHEDRAL is used. The input files and running script can be found here: polyproline-1d-abmd.

The initial coordinates have been prepared by a SMD along the path of the collective variable. Two steps of ABMD have been carried out:

Step1: Run a coarse ABMD simulation with the resolution of CV set 0.2. Eight replicas are used. The pseudo-temperature is set 10000K.

Step2: Follow up with a finer ABMD run with the resolution of CV set 0.1, using the biasing potential from Step 1.

The resultant 1D Free Energy curve is:

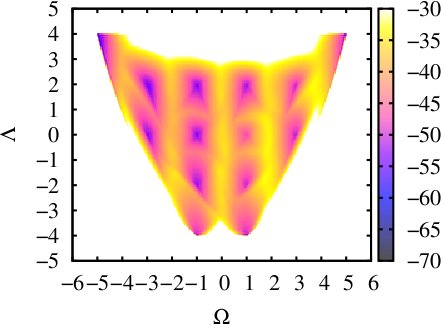
(iii) Calculating a 2-d free energy landscape of a proline pentapeptide

This is the extension of last example to the two dimensional case. Here we choose another CV as PAIR_OF_DIHEDRAL(for the definition of this CV you can check [13]). We run a 50ns ABMD with the well-tempered algorithm in an explicit solvent environment, using the same initial coordinates as in the last example. The resolution of CVs are both set 0.2 and the pseudo-temperature is set 10000K. The input files and running script can be found here: polyproline-2d-abmd.

The result gives the 2-D Free Energy landscape as follows, which shows similar pattern with the one in [13].

References

[1] A. Laio, and M. Parrinello, "Escaping free-energy minima", Proc. Natl. ACad. Sci. USA 99, 12562 (2002).

[2] M. Iannuzzi, A. Laio, and M. Parrinello, "Efficient exploration of reactive potential energy surfaces using Car-Parrinello molecular dynamics", Phys. Rev. Lett. 90, 238302 (2003).

[3] V. Babin, C. Roland, and C. Sagui, "Adaptively biased molecular dynamics for free energy calculations", J. Chem. Phys. 128, 134101 (2008).

[4] V. Babin, V. Karpusenka, M. Moradi, C. Roland, and C. Sagui, "Int. J. Quant. Chem. 109, 3666 (2009).

[5] M. Moradi, V. Babin, C. Roland and C. Sagui, "The adaptively biased molecular dynamics method revisited: new capabilities and an application", J. Phys. Conf. Ser. 640, 012020 (2015).

[6] S. Izrailev, S. Stepaniants, B. Isralewitz, B. Kosztin, H. Lu, F. Molnar, W. Wriggers, and K. Schulten, "Steered molecular dyanmics", in Computational Molecular Dynamics: Challenges, Methods, Ideas", Springer Verlag, Berlin, Germany 1998.

[7] Y, Suguta, A. Kitao, and Y. Okamoto, "Multidimensional replica-exchange method for free energy calculations", J. Phys. Chem. 113, 6042 (2000).

[8] A. Pan, D. Sezer, and B. Roux, "Finding transition pathways using the string method with swarms of trajectories", J. Phys. Chem. B 112, 3432 (2008).

[9] K. Minoukadeh, Ch. Chipot, and T. lelievre, "Potential of mean force calculations: A multiple walker adaptive biasing force technique", J. Chem. Theor. and Comput. 6, 1008 (2010).

[10] A. Barducci, G. Bussi, and M. Parrinello, "Well-tempered metadynamics: a smoothly converging and tunable free energy method", Phys. Rev. Lett. 100, 020603 (2008).

[11] M. Moradi, and E. Tajkorshid, "Driven metadynamics: reconstructing equilibrium free energies from driven adaptive-bias simulations", J. Phys. Chem. Lett. 4, 1882 (2013).

[12] V. Babin and C. Sagui, "Conformational free energies of methyl-alpha-L-iduronic and methyl-beta-D-glucuronic acids in water", J. Chem. Phus. 132, 104108 (2010).

[13] M. Moradi, V. Babin, C. Roland, T. Darden and C. Sagui, "Conformations and free energy landscapes of polyproline peptides", Proc. Natl. Acad. Sci. USA 106, 20746 (2009).

[14] M. Moradi, V. Babin, C. Roland and C. Sagui, "A classical molecular dynamics investigation of the free energy and structure of short polyproline conformers", J. Chem. Phys. 133, 125104 (2010).

[15] M. Moradi, J.-G. Lee, V. Babin, C. Roland, and C. Sagui, "Free energy and structure of polyproline peptides: an ab intio and classical molecular dynamics investigation", Int. J. Quant. Chem. 110, 2865 (2010).

[16] M. Moradi, V. Babin, C. Sagui, and C. Roland, "A statistical analysis of the PPII propensity of amino acids guests in proline-rich peptides", Biophysical J. 100, 1083 (2011).

[17] M. Moradi, V. Babin, C. Sagui, and C. Roland, " PPII propensity of multiple-guest amino acids in a proline-rich environment", J. Phys. Chem. B 115, 8645 (2011).

[18] M. Moradi, V. Babin, C. Roland, and C. Sagui, "Are long-range structural correlations behind the aggregation phenomena of polyglutamine diseases?", PLoS Comput. Biol. 8, e1002501 (2012).

[19] M. Moradi, V. Babin, C. Roland and C. Sagui, "Reaction path ensemble of the B-Z-DNA transition: a comprehensive atomistic study", Nucl. Acids. Res. 41, 33 (2013).